The Law of Cosines

So we recently covered the Pythagorean Theorem, and I am betting you’ve got at least one concern. No, I don’t mean about whether or not Planet X has begun cutting a destructive swath across our solar system. I mean in regards to calculating the length of the side of a triangle if you know the other two. Don’t have a right triangle? You may think you’re SOL. I am here to tell you there is hope. Enter the Law of Cosines.

The Law of Cosines

(1) $\begin{equation*} c^2 = a^2 + b^2 - 2abcosC \end{equation*}$

“Wait a minute!” you may be thinking. “The LAW of cosines?! Why did we bother with Pythagoras and his measly theorem when we had a capital L Law at our disposal?”

Well, while it is true that the Law of Cosines allows us to calculate lengths of sides for non-right triangles, the truth is that is that it is based on the Pythagorean Theorem and not vice versa as some might expect. Let me explain.

Deriving the Law of Cosines

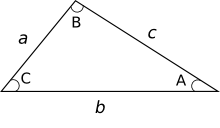
Consider the following triangle:

This triangle has three sides: a, b, and c. The angles are named respective to the side they are opposite: A, B, and C. We know the lengths of sides a and b, and we know the size of angle C. We want to calculate the length of side c. How can we do it?

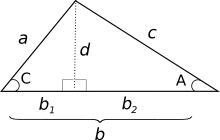
Well, it’s not a right triangle so we can’t use the Pythagorean Theorem. Or can we? Let’s drop a line from vertex B down and perpendicular to side b.

Now we’ve got something we can work with! Specifically, we have two right triangles that share a common side, d. Note that I’ve also divided side b into sides b₁ and b₂. With the Pythagorean Theorem, some trig and some algebra we should now be able to solve for c.

Looking the right triangle dcb₂, we know by the Pythagorean Theorem that:

$c^2 = b_2^2 + d^2$

That looks like a good start. We’ve got an equation for $c^2$ , and we’ve got two terms, $b_2$ and $d$ that we can redefine in terms of our known angle C using the the definitions of sine and cosine on the right triangle adb₁.

$d$ is easy:

$d = asinC$

$b_2$ is a little trickier since it is related to $b_1$ through $b$ . Specifically, we know that $b_1 + b_2 = b$ so,

$b_2 = b - b_1$

Unfortunately, while we know b (that’s how we defined our problem), we do not know $b_1$ . We can use the definition of cosine, though:

$b_1 = acosC$

So,

$b_2 = b - acosC$

Now that we have $b_2$ and $d$ defined in terms of known values, we can substitute both back into our equation for $c^2$ , i.e., the Pythagorean Theorem applied to triangle dcb₂.

$c^2 = (asinC)^2 + (b - acosC)^2$

Hopefully expanding then simplifying the above will get us where we need to go:

$c^2 = a^2sin^2C + b^2 - 2abcosC + a^2cos^2C$

$c^2 = a^2sin^2C + a^2cos^2C + b^2 - 2abcosC$

$c^2 = a^2(sin^2C + cos^2C) + b^2 - 2abcosC$

$c^2 = a^2 + b^2 -2abcosC$

There you have it, the Law of Cosines. You’ll notice that the Pythagorean Theorem is a degenerate instance of this. When $C$ is 90 degrees, $cosC$ is zero making that whole last term equal to zero, leaving you with $c^2 = a^2 + b^2$ . And even though the Pythagorean Theorem is a special case of the Law of Cosines, the Pythagorean Theorem was integral, along with the definitions of sine and cosine, for deriving the more general Law of Cosines.

The Law of Cosines

Deriving the Law of Cosines

Leave a Reply Cancel reply

Recent Posts

On Twitter