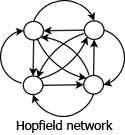
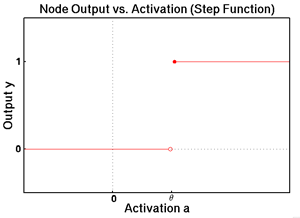
This is the second article in the series about artificial neural networks. If you have not already done so, I recommend you read the first article, “Neural Networks: The Node“, before proceeding. It covers material that should be understood before attempting to tackle the topics presented here and in future articles in this series. There …
Tag: neural dump
May 08 2016
Neural Networks: The Node
As I covered previously in “Introduction to Neural Networks,” artificial neural networks (ANN) are simplified representations of biological neural networks in which the basic computational unit known as an artificial neuron, or node, represents its biological counterpart, the neuron. In order to understand how neural networks can be taught to identify and classify, it is first …
Mar 09 2016
Unsigned Binary Integers and Internal Congruence
This is going to be another one of my “selfish” posts – written primarily for me to refer back to in the future and not because I believe it will benefit anyone other than me. The idea is one that I always took for granted but had a hard time proving to myself once I decided …
Jan 14 2016
Proof of the Power Rule
If you’ve got the word “power” in your name, you’d better believe expectations are going to be sky high for what you can do. The Power Rule in calculus brings it and then some. The Power Rule, probably the most used rule when differentiating, gives us a drop dead simple way to differentiate polynomials. Specifically …
Aug 28 2015
The Law of Cosines
So we recently covered the Pythagorean Theorem, and I am betting you’ve got at least one concern. No, I don’t mean about whether or not Planet X has begun cutting a destructive swath across our solar system. I mean in regards to calculating the length of the side of a triangle if you know the other …
Aug 13 2015
Pythagorean Theorem Proof
It may very well be the second most famous equation of all time, outshone only by that braggart Einstein’s mass–energy equivalence equation. But for those of us that aren’t theoretical physicists, the Pythagorean Theorem is likely to play a fundamental role in many of the calculations we do whether we realize it or not. Everyone knows …
Dec 27 2014
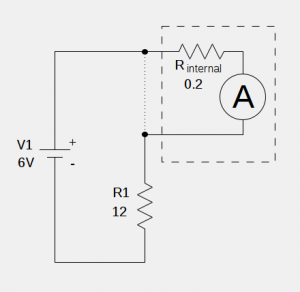
Ammeters and Internal Resistance
Question: Based on your previous post regarding voltmeters and internal resistance, I can safely assume that an ammeter must also have some internal resistance. What effect does this resistance have on current measurements, and what resistance value would minimize any error it introduces to the reading? Answer: It is indeed true that an ammeter must …
Nov 24 2014
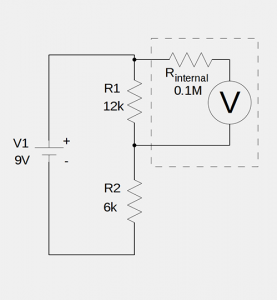
Voltmeters and Internal Resistance
Question: Does a voltmeter have any internal resistance, and if so, what, if any, affect does it have on voltage readings? Answer: Even if you have no electrical experience at all, I would hope that your answer to the first part of the question was, “yes.” Otherwise this would turn out to be an incredibly short …
Nov 15 2014
Euler’s Formula
Besides being an obvious lady killer, Swiss mathematician Leonhard Euler gifted the world with some pretty important mathematical concepts, notational conventions, and formulas. I almost feel bad about the fact that I couldn’t even spell his name correctly until I was well into adulthood. You are probably thinking, “Sure, he had a bitchin’ robe, and for …
Nov 10 2014
Complex Numbers and their Geometry
(Note: I lied. This will be my first “neural dump.” I began writing about Euler’s Formula, but felt what follows was worthy of its own post and a better foundation for what will follow when I tackle Euler.) Complex numbers arose from the fact that there is no solution for in the equation in , …
- 1
- 2