Sep 21 2017
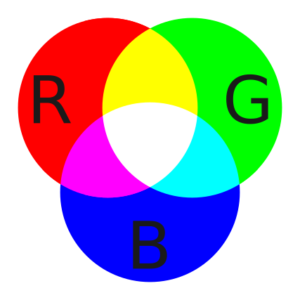
If you are an artist, photographer, graphic designer, or web developer, having a firm understanding of colors is a necessity. Key to being able to study and discuss colors is a formal framework for quantizing their properties. Abstract mathematical models called color models do just this, allowing people to discuss the qualities of a color …
Jan 29 2017
Abraham Lincoln once famously said, “Everybody loves a compliment.” I suspect that if he had been a mathematician he would have loved complements, too. We’ve already seen what complements are and talked about the two most prolific: the radix complement and the diminished radix complement. Now it’s time to explore how we can leverage complements …
Jan 10 2017
In my last post about binary signed integers, I introduced the ones complement representation. At the time, I said that the ones complement was found by taking the bitwise complement of the number. My explanation about how to do this was simple: invert each bit, flipping 1 to 0 and vice versa. While it’s true that …
